Question

Learning Goal: To learn the definition and applications of angular momentum including its relationship to torque. By now, you should be familiar with the concept of momentum, defined as the product of an object's mass and its velocity: p⃗ =mv⃗ . You may have noticed that nearly every translational concept or equation seems to have an analogous rotational one. So, what might be the rotational analogue of momentum? Just as the rotational analogue of force F⃗ , called the torque τ⃗ , is defined by the formula τ⃗ =r⃗ ×F⃗ , the rotational analogue of momentum p⃗ , called the angular momentum L⃗ , is given by the formula L⃗ =r⃗ ×p⃗ , for a single particle. For an extended body you must add up the angular momenta of all of the pieces. There is another formula for angular momentum that makes the analogy to momentum particularly clear. For a rigid body rotating about an axis of symmetry, which will be true for all parts in this problem, the measure of inertia is given not by the mass m but by the rotational inertia (i.e., the moment of inertia) I. Similarly, the rate of rotation is given by the body's angular speed, ω. The product Iω⃗ gives the angular momentum L⃗ of a rigid body rotating about an axis of symmetry. (Note that if the body is not rotating about an axis of symmetry, then the angular momentum and the angular velocity may not be parallel.)

Answer 1

Let's analyse the definition and applications of angular momentum, and its relation with torque.

First of all, it's important to consider that the angular momentum is a property of rotational dynamics. Also, it's the analogue of the linear momentum.

Mathematically, the angular momentum is defined as

`L=r * p`

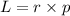
Where
`L` represents the angular momentum vector,
`r` represents is the position vector and
`p` is the linear momentum vector.

Notice that the angular momentum is also a vector, which is the cross product of two vectorial magnitudes. In other words, the direction of the resulting vector (linear momentum) follows the right hand rule, which means that the resulting direction is according to the rotation direction, also means that the cross product is not commutative, which is a common assumption students make.

Now, the realtion between angular momentum and torque is that the change of the angular momentum with respect to time is equivalent to its torque:

`(d)/(dt)[L]=(d)/(dt)[r * p] =\tau`

Remember that torque is defined as
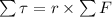`\sum \tau = r * \sum F`, and the derivative of the cross product is

`(d)/(dt)[L]=(d)/(dt)[r * p] = (dr)/(dt) * p + r * (dp)/(dt)`

Then,

`(d)/(dt)[L] =(v * mv)+r * (dp)/(dt)`

But,
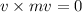`v * mv = 0`, because those vector are parallel.

So,
`(d)/(dt)[L] = r* \sum F = \tau`

At this point, we demonstrate it the relation between torque and rotational momentum.

In words, the net torque on a particle is equal to the rate of change of the angular momentum with respect to time.

Now, the application of angular momentum can be seen in skating spins, notice that when the skater puts his arms closer to its body, he'll rotate faster. The reason of this phenomenon is because arms represents rotating mass and the axis is the body, so the postion of this arm mass changes to zero distance to the rotational axis, that will increase the angular momentum, making higher. If the angular momentum is higher, the torque will be also higher, that's way the skater increses its rotational velocity.