Question

Rotational dynamics about a fixed axis: A solid uniform sphere of mass 1.85 kg and diameter 45.0 cm spins about an axle through its center. Starting with an angular velocity of 2.40 rev/s, it stops after turning through 18.2 rev with uniform acceleration. The net torque acting on this sphere as it is slowing down is closest to:A) 0.149 N m. B) 0.0620N m. C) 0.00593 N m. D) 0.0372 N m. E) 0.0466 N·m

Answer 1

(D) The net torque acting on this sphere as it is slowing down is closest to 0.0372 N.m

Step-by-step explanation:

Given;

mass of the solid sphere, m = 1.85 kg

radius of the sphere, r = ¹/₂ of diameter = 22.5 cm

initial angular velocity, ω = 2.40 rev/s = 15.08 rad/s

angular revolution, θ = 18.2 rev = 114.37 rad

Torque on the sphere, τ = Iα

Where;

I is moment of inertia

α is angular acceleration

Angular acceleration is calculated as;

`\omega_f^2 = \omega_i^2 +2 \alpha \theta\\\\0 = 15.08^2 + (2*114.37)\alpha\\\\\alpha = (-15.08^2)/((2*114.37)) = -0.994 \ rad/s^2\\\\\alpha = 0.994 \ rad/s^2 \ (in \ opposite \ direction)`

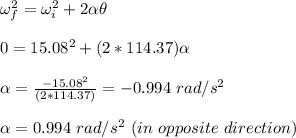
moment of inertia of solid sphere, I = ²/₅mr²

= ²/₅(1.85)(0.225)²

= 0.03746 kg.m²

Finally, the net torque on the sphere is calculated as;

τ = Iα

τ = 0.03746 x 0.994

τ = 0.0372 N.m

Therefore, the net torque acting on this sphere as it is slowing down is closest to 0.0372 N.m

Answer 2

D) 0.0372 N m

Step-by-step explanation:

r = 45/2 cm = 22.5 cm = 0.225 m

As 1 revolution = 2π rad we can convert to radian unit

2.4 rev/s = 2.4 * 2π = 15.1 rad/s

18.2 rev = 18.2 * 2π = 114.35 rad

We can calculate the angular (de)acceleration using the following equation of motion

`-\omega^2 = 2\alpha \theta`

`- 15.1^2 = 2*\alpha * 114.35`

`\alpha = (-15.1^2)/(2*114.35) = -0.994 rad/s^2`

The moment of inertia of the solid uniform sphere is

`2mr^2/5 = 2*1.85*0.225^2/5 = 0.0375 kgm^2`

The net torque acting on this according to Newton's 2nd law is

`T = I\alpha = 0.0375 * 0.994 = 0.0372 Nm`