Answer:
The particle's velocity is 212.15 m/s.
Step-by-step explanation:
Given that,
Charge of particle,
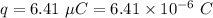
The magnitude of electric field, E = 1270 N/C
The magnitude of magnetic field, B = 1.28 T
Net force,
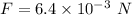
We need to find the magnitude of the particle's velocity. the net force acting on the particle is given by Lorentz force as :
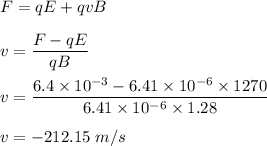
So, the particle's velocity is 212.15 m/s.