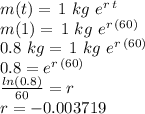Question

A radioactive substance decays at a rate proportional to the amount (mass) that is present. Denote the proportionality constant by the letter r. Suppose we start with 1 kg of the substance. (a) (1pt) Write the differential equation and initial condition for the mass m(t) of the substance as a function of time t (measured in hours). (b) (1pt) Find the solution as a function of t and r. (c) (1pt) Suppose that, one hour later, 0.8 kgs remain. Find The constant r. (d) (1pt) Suppose we measure time in minutes. Find the differential equation for m(s), if s denotes time in minutes.

Answer 1

a) The differential equation is:
`(dm)/(dt) =r\,m`

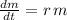
with initial condition:
`m(0)=1\,\,kg`

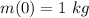
b) m(t) =\,1\,\,kg\,\,e^{r\,t}

c) r=-0.22314

d) Same differential equation, but the solution function would have a different value for "r" resultant from dividing by 60:
`(ln(0.8))/(60) =r\\r=-0.003719`

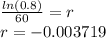
Explanation:

Part a)

The differential equation is:
`(dm)/(dt) =r\,m`

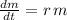
with initial condition:
`m(0)=1\,\,kg`

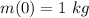
Part b)

The solution for a function whose derivative is a multiple of the function itself, must be associated with exponential of base "e":

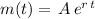`m(t) =\,A\,e^(r\,t)` with
`A = m(0) = 1\,\,kg`

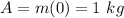
So we can write the function as:
`m(t) =\,1\,\,kg\,\,e^(r\,t)`

Part c)

To find the constant "r", we use the information given on the amount of substance left after one hour (0.8 kg) by using t = 1 hour, and solving for "r" in the equation:

`m(t) =\,1\,\,kg\,\,e^(r\,t)\\m(1) =\,1\,\,kg\,\,e^(r\,(1))\\0.8\,\,kg=\,1\,\,kg\,\,e^(r\,(1))\\0.8=e^(r\,(1))\\ln(0.8)=r\\r=-0.22314`

where we have rounded the answer to the 5th decimal place. Notice that this constant "r" is negative, associated with a typical exponential decay.

Part d)

The differential equation if we measure the time in minutes would be the same, but its solution would have a different constant "r" given by the answer to the amount of substance left after 60 minutes have elapsed:

`m(t) =\,1\,\,kg\,\,e^(r\,t)\\m(1) =\,1\,\,kg\,\,e^(r\,(60))\\0.8\,\,kg=\,1\,\,kg\,\,e^(r\,(60))\\0.8=e^(r\,(60))\\(ln(0.8))/(60) =r\\r=-0.003719`