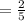Question

(5 points) An urn contains two blue balls denoted by B1 and B2, and three white balls denoted by W1, W2 and W3. One ball is drawn,, its color is recorded and it is replaced in the urn. Then the second ball is drawn and its color is recorded. Consider the event that the first ball that is drawn is blue. List all outcomes in the event. What is the probability of the event?

Answer 1

The probability of the event that first ball that is drawn is blue is
`\frac 25`.

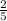Explanation:

Probability:

If S is is an sample space in which all outcomes are equally likely and E is an event in S, then the probability of E,denoted P(E) is

`P(E)=\frac{\textrm{The number of outcomes E}}{\textrm{The total number outcomes of S}}`

Given that,

An urn contains two balls B₁ and B₂ which are blue in color and W₁,W₂ and W₃ which are white in color.

Total number of ball =(2+3) =5

The number ways of selection 2 ball out of 5 ball is

=5²

=25

Total outcomes = 25

List of all outcomes in the event that the first ball that is drawn is blue are

B₁B₁ , B₁B₂ , B₁W₁ , B₁W₂ , B₁W₃ , B₂B₁ , B₂B₂ , B₂W₁ , B₂W₂ , B₂W₃

The number of event that the first ball that is drawn is blue is

=10.

The probability of the event that first ball that is drawn is blue is

`=(10)/(25)`

`=\frac25`