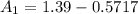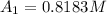Answer:
The concentration at the cathode is
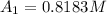
Step-by-step explanation:
From the question we are told that
The initial concentration is
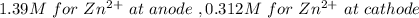
The reaction is
At Cathode
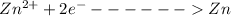
At anode
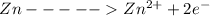
The initial potential is
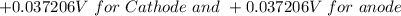
The complete reaction is
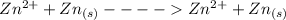
(Cathode) ----------------- (anode)
Looking the reaction above we can see that after the reaction
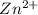 at cathode loss some concentration and
at cathode loss some concentration and
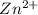 will gain some concentration
will gain some concentration
Let say the amount of concentration lost/gained is = z M
The after the reaction the concentration of
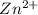 at the cathode would be
at the cathode would be

While the concentration at the anode would be
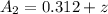
At initial the condition the net potential of the cell is
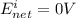
After time

The potential of the cell is

Generally this potential is defined by Nernst equation as
![E_(cell) = E^i_(cell)- (RT)/(nF) ln[([A_2])/([A_2]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/c94igsg9fm0zq36ny4rasplj0w3elpbv1q.png)
Where R is the gas constant with a value of
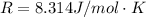
T is the temperature given as
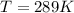
n is the number of mole of electron which

F is the farad constant with a value of
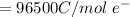
Substituting values
![0.0095376 =0.0 -([8.314][288])/([2] [9600]) ln [((0.312 +z))/((1.39 -z)) ]](https://img.qammunity.org/2021/formulas/chemistry/college/euai56olhho9ot7lkyb0x0pzj0ih2rkyty.png)
![0.0095376 = 0.12406383 \ ln [(( 0.312 + z))/([1.39 -z]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/haxahhu94og8d61e2ajysvwvbfw4hyrq4d.png)
![(0.0095376 )/( 0.12406383) = \ ln [(( 0.312 + z))/([1.39 -z]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/xxf1c4lj1pyw4kswudhzjtw8ox6667kj5a.png)
![0.0768766 = \ ln [(( 0.312 + z))/([1.39 -z]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/e1d04rwrzdyv04i10aui4pcq1r1jdg0ozz.png)
Taking exponent of both sides
![e^(0.0768766 )= [(( 0.312 + z))/([1.39 -z]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/uuzk4fozy16kxle7t9aybpk2cjwdznjsct.png)
![1.0799 = [(( 0.312 + z))/([1.39 -z]) ]](https://img.qammunity.org/2021/formulas/chemistry/college/3fvfg9d83sgvrk180d8mm8dahhpr2wx3n3.png)
![[1.39 -z ]1.0799 = 0.312 + z \\\\1.501 - 1.0799z = 0.312 +z\\\\1.501-0.312 = 1.0799z + z\\\\1.1891 =2.0799z\\\\ z =(1.1891)/(2.0799)\\\\ z =0.5717](https://img.qammunity.org/2021/formulas/chemistry/college/s4yooxj26tzxjg0k3u6k9afnrt8a0dejuf.png)
The concentration at the cathode is