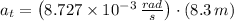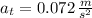Answer:
1)
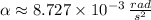 , 2)
, 2)
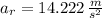 , 3)
, 3)
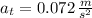
Step-by-step explanation:
1) Let consider that Apollo spacecraft accelerates at constant rate. The angular acceleration of the spacecraft is:
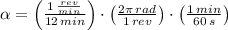
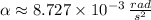
2) The angular speed of the Apollo spacecraft at t = 2.5 min is:
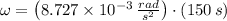

The radial component of the linear acceleration is:
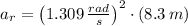
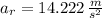
3) The tangential component of the linear acceleration is