A city has a population of 50,000 in 2012. If the population of the city grows at an annual rate of 2%, the year in which the population will reach 100,000 is _____________ and …

Question

asked Apr 4, 2021 26.0k views

1 Answer

Twil · Answer 1 · 2021-04-11T10:03:44+0000

Answer:

The population will reach 100,000 in 2047.

The population will reach 200,000 in 2082.

Explanation:

The compounded growth formula:

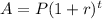
A=P(1+r)^t

A= Population after t years

P= Initial amount of population

r= rate of growth

t= Time in years

Given that,

P=50,000, r=2% =0.02, A=100,000

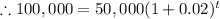
$\therefore 100,000=50,000(1+0.02)^t$

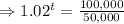
$\Rightarrow 1.02^t=(100,000)/(50,000)$

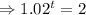
$\Rightarrow 1.02^t=2$

Taking ln both sides

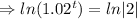
$\Rightarrow ln(1.02^t)=ln|2|$

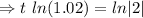
$\Rightarrow t\ ln(1.02)=ln|2|$

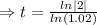
$\Rightarrow t=(ln|2|)/( ln(1.02))$

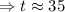
$\Rightarrow t\approx 35$

The population will reach 100,000 in (2012+35)=2047

P=50,000, r=2% =0.02, A=200,000

$\therefore 200,000=50,000(1+0.02)^t$

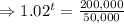
$\Rightarrow 1.02^t=(200,000)/(50,000)$

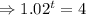
$\Rightarrow 1.02^t=4$

Taking ln both sides

$\Rightarrow ln(1.02^t)=ln|4|$

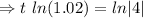
$\Rightarrow t\ ln(1.02)=ln|4|$

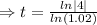
$\Rightarrow t=(ln|4|)/( ln(1.02))$

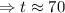
$\Rightarrow t\approx 70$

The year it will reach 200,000 is (2012+70)=2082