Question

A child of mass 53.7 kg sits on the edge of a merry-go-round with radius 2.2 m and mo- ment of inertia 205.327 kgm2. The merry- go-round rotates with an angular velocity of 1.6 rad/s. The child then walks towards the center of the merry-go-round and stops at a distance 0.836 m from the center. Now what is the angular velocity of the merry-go-round? Answer in units of rad/s.

Answer 1

2.068 rad/s.

Step-by-step explanation:

Given,

mass of child, m = 53.7 Kg

radius of merry-go-round, r = 2.2 m

moment of inertia of merry-go-round,I = 205.327 kgm²

Initial angular speed, ω = 1.6 rad/s

distance moved by the child, r' = 0.836 m

Using conservation of angular momentum

`(I + I_1)\omega_1 = (I + I_2) \omega_2`

`(205.327+ 53.7* 2.2)* 1.6 = (205.327 + 53.7* 0.836) \omega_2`

`\omega_2 = 2.068\ rad/s`

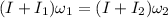
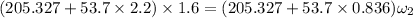
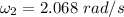
The new angular speed of the merry-go-round when child moves inside is equal to 2.068 rad/s.