Question

A 1.2-m radius cylindrical region contains a uniform electric field along the cylinder axis. It is increasing uniformly with time. To obtain a total displacement current of 2.0x10-­9 A through a cross section of the region, the magnitude of the electric field should change at a rate of:

Answer 1

The magnitude of rate of change of electric field is
`49.95\ V/m{\cdot} s`.

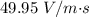Step-by-step explanation:

Given that,

Radius of the cylindrical region contains a uniform electric field along the cylinder axis, r = 1.2 m

Total displacement current through a cross section of the region,
`I=2* 10^(-9)\ A`

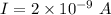
We need to find the rate of change of electric field. Its is given by the formula as follows :

`(dE)/(dt)=(I)/(A\epsilon_o)\\\\(dE)/(dt)=(2* 10^(-9))/(\pi (1.2)^2* 8.85* 10^(-12))\\\\(dE)/(dt)=49.95\ V/m{\cdot} s`

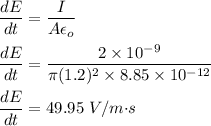
So, the magnitude of rate of change of electric field is
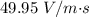`49.95\ V/m{\cdot} s`.