Complete Question: The complete question is in the file attached to this solution
Answer:
a)
![\left[\begin{array}{ccc}45&24\\67&89\end{array}\right] =\left[\begin{array}{ccc}X_(1) \\X_(2) \end{array}\right] + \left[\begin{array}{ccc}155.25 \\397.80 \end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/mi705m24rpyd8jskfgp8gezw9zrn2y6qje.png)
b) The new hire sold a small drink for $1.78 and a medium drink for $3.13
Explanation:
The matrix vector equation can be written as:
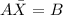 ............(1)
............(1)
let X₁ = Price of small drinks
Let X₂ = Price of medium drinks
The vector
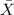 of the prices of small and medium drinks is:
of the prices of small and medium drinks is:
![\bar{X} = \left[\begin{array}{ccc}X_(1) \\X_(2) \end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/2mw8h49aljc8apxxmxgxiv4fje4mmjvta4.png)
The matrix of the total sales can be written as:
![A = \left[\begin{array}{ccc}45&24\\67&89\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/k83ppsfs72r91trodx6cric0ehv1dhamtp.png)
![B = \left[\begin{array}{ccc}155.25 \\397.80 \end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/4zfd1xz29yk31gui09glajihrbozdf6eae.png)
According to the equation written in (1), the matrix vector equation is:
![\left[\begin{array}{ccc}45&24\\67&89\end{array}\right] =\left[\begin{array}{ccc}X_(1) \\X_(2) \end{array}\right] + \left[\begin{array}{ccc}155.25 \\397.80 \end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/mi705m24rpyd8jskfgp8gezw9zrn2y6qje.png)
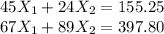
Solving for X₁ and X₂ in the equations above:
X₁ = 1.78
X₂ = 3.13