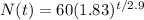Answer:
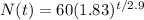
Explanation:
If an initial number of branches
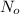 increases at a rate r% for a duration of t years in k periods, the Number of branches (N(t) at any time t will be modeled by the equation:
increases at a rate r% for a duration of t years in k periods, the Number of branches (N(t) at any time t will be modeled by the equation:
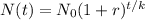
Initially Bela's tree had 60 branches, therefore,
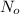 =60.
=60.
Rate of Increase, r=83%=0.83
Period, k=2.9 Years
Therefore, the number of branches (after t years)

The function that models the number of branches t years since Bela began studying her tree is