Question

A composite figure is formed from a cone and a cylinder with the same base radius, and its volume can be calculated by multiplying the volume of the cylinder by a rational number, a/b. What arrangements of the cylinder and cone could explain this?

Answer 1

The composite figure comprises of a cone balanced on top of cylinder

Explanation:

The composite figure is formed from a cone and a cylinder with the same base radius, Let the base radius be r

Then the volume of the cone will be
`V_(cone)`

Then the volume of the cylinder will be
`V_(cylinder)`

`V_(cylinder) = \pi r^(2) h_(cylinder)`

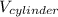
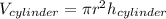
The total volume of the composite figure will be V, where

`V= V_(cone) + V_(cylinder)`

`V = (1)/(3) \pi r^(2) h_(cone) +\pi r^(2) h_(cylinder)`

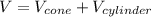
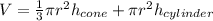
let the height of cone and cylinder be same

The volume of the composite figure will be
`(4)/(3) \pi r`
`r^(2) h`

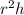
Hence
`(4)/(3) = (a)/(b)`

Thecomposite figure comprises of a cone balanced on top of cylinder