Answer:
The Volume is decreasing at a rate of

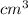 per minute.
per minute.
Explanation:
Given a cone of radius r and perpendicular height h
Volume of the cone,

Since the height of the cone is fixed, the rate of change of the volume of the Cone,
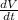 is given as:
is given as:
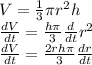
We are to determine the rate of change of the Volume, V when:
The radius is decreasing at a rate of 2 cm per minute,
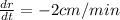
Height, h=9 cm
Radius = 13cm
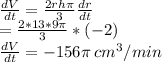
The Volume is decreasing at a rate of

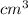 per minute.
per minute.