The equation of the line that passes through the point (3,4) and is parallel to the line shown is:
-
 (option B)
(option B)
How to obtain the equation of the line?
Step 1: Determine the slope of the line shown in the graph. Details below:
- x₁ = 0
- x₂ = 4
- y₁ = 1
- y₂ = 2
- Slope of line (m₁) =?

Now, we shall obtain the equation of the parallel to the line shown in the question. Details below:
- Slope of line shown (m₁) =
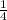
- Slope of the line parallel to the line shown (m₂) = m₁ =
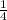
- Coordinate of the line = (3, 4)
- x coordinate 1 (x₁) = 3
- y coordinate 1 (y₁) = 4
- Equation of line =?

Thus, the correct answer is option B