Question

Sphere A with mass 80 kg is located at the origin of an xy coordinate system; sphere B with mass 60 kg is located at coordinates (0.25 m, 0); sphere C with mass 0.20 kg is located in the first quadrant 0.20 m from A and 0.15 m from B. In unit-vector notation, what is the gravitational force on C due to A and B?

Answer 1

Fc = [ - 4.45 * 10^-8 j ] N

Step-by-step explanation:

Given:-

- The masses and the position coordinates from ( 0 , 0 ) are:

Sphere A : ma = 80 kg , ( 0 , 0 )

Sphere B : ma = 60 kg , ( 0.25 , 0 )

Sphere C : ma = 0.2 kg , ra = 0.2 m , rb = 0.15

- The gravitational constant G = 6.674×10−11 m3⋅kg−1⋅s−2

Find:-

what is the gravitational force on C due to A and B?

Solution:-

- The gravitational force between spheres is given by:

F = G*m1*m2 / r^2

Where, r : The distance between two bodies (sphere).

- The vector (rac and rbc) denote the position of sphere C from spheres A and B:-

Determine the angle (α) between vectors rac and rab using cosine rule:

`cos ( \alpha ) = (rab^2 + rac^2 - rbc^2)/(2*rab*rac) \\\\cos ( \alpha ) = (0.25^2 + 0.2^2 - 0.15^2)/(2*0.25*0.2)\\\\cos ( \alpha ) = 0.8\\\\\alpha = 36.87^(\circ \:)`

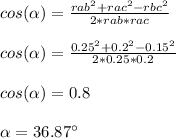
Determine the angle (β) between vectors rbc and rab using cosine rule:

`cos ( \beta ) = (rab^2 + rbc^2 - rac^2)/(2*rab*rbc) \\\\cos ( \beta ) = (0.25^2 + 0.15^2 - 0.2^2)/(2*0.25*0.15)\\\\cos ( \beta ) = 0.6\\\\\beta = 53.13^(\circ \:)`

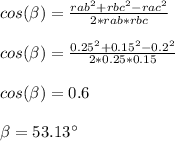
- Now determine the scalar gravitational forces due to sphere A and B on C:

Between sphere A and C:

Fac = G*ma*mc / rac^2

Fac = (6.674×10−11)*80*0.2 / 0.2^2

Fac = 2.67*10^-8 N

vector Fac = Fac* [ - cos (α) i + - sin (α) j ]

vector Fac = 2.67*10^-8* [ - cos (36.87°) i + -sin (36.87°) j ]

vector Fac = [ - 2.136 i - 1.602 j ]*10^-8 N

Between sphere B and C:

Fbc = G*mb*mc / rbc^2

Fbc = (6.674×10−11)*60*0.2 / 0.15^2

Fbc = 3.56*10^-8 N

vector Fbc = Fbc* [ cos (β) i - sin (β) j ]

vector Fbc = 3.56*10^-8* [ cos (53.13°) i - sin (53.13°) j ]

vector Fbc = [ 2.136 i - 2.848 j ]*10^-8 N

- The Net gravitational force can now be determined from vector additon of Fac and Fbc:

Fc = vector Fac + vector Fbc

Fc = [ - 2.136 i - 1.602 j ]*10^-8 + [ 2.136 i - 2.848 j ]*10^-8

Fc = [ - 4.45 * 10^-8 j ] N