Explanation:
Area, A = Length,x × Breadth,y
A=xy
When x and y are independent, E(xy) = E(x)E(y)
As x and y have the same distribution, U[L-A,L+A], they have the same mean.
We could argue by symmetry that E(x) = L and E(y) + L, also.
We can also reason this from the fact that, if X ~ U[L-A, L+A], f(x) = 1/(2A) from L-A to L+A
Therefore
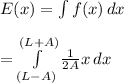
![=\int\limits^((L+A))_((L-A)) {(1)/(2A)x } \, dx \\\\=[(1)/(4A)x^2 ]\limits^((L+A))_((L-A))](https://img.qammunity.org/2021/formulas/mathematics/college/ybpep4pc9glbteshwawwkislmin623gyot.png)
=1/(4A)(L+A)2 - 1/(4A)(L-A)2
= 1/(4A)(L2 + 2AL + A2) - 1/(4A)(L2 - 2AL + A2)
=1/(4A)(2AL+2AL)
= 1/(4A)(4AL)
= L
Thus, E(xy) = E(x)E(y) = L×L = L²