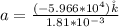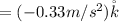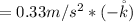Question

To practice Problem-Solving Strategy 27.1: Magnetic Forces. A particle with mass 1.81×10−3 kgkg and a charge of 1.22×10−8 CC has, at a given instant, a velocity v⃗ =(3.00×104m/s)j^v→=(3.00×104m/s)j^. What are the magnitude and direction of the particle’s acceleration produced by a uniform magnetic field B⃗ =(1.63T)i^+(0.980T)j^B→=(1.63T)i^+(0.980T)j^?

Answer 1

The magnitude of the acceleration is
`a = 0.33 m/s^2`

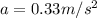
The direction is
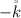`- \r k` i.e the negative direction of the z-axis

Step-by-step explanation:

From the question we are that

The mass of the particle
`m = 1.8*10^(-3) kg`

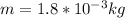
The charge on the particle is
`q = 1.22*10^(-8)C`

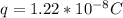
The velocity is
`\= v = (3.0*10^4 m/s ) j`

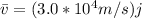
The the magnetic field is
`\= B = (1.63T)\r i + (0.980T) \r j`

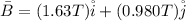
The charge experienced a force which is mathematically represented as

`F = q (\= v * \= B)`

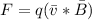
Substituting value

`F = 1.22*10^(-8) (( 3*10^4 ) \r j \ \ X \ \ ( 1.63 \r i + 0.980 \r j )T)`

`= 1.22 *10^(-8) ((3*10^4 * 1.63)(\r j \ \ X \ \ \r i) + (3*10^4 * 0.980) (\r j \ \ X \ \ \r j))`

`= (-5.966*10^4 N) \r k`

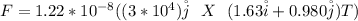
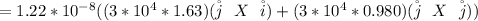
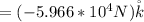
Note :

`i \ \ X \ \ j = k \\\\j \ \ X \ \ k = i\\\\k \ \ X \ \ i = j\\\\j \ \ X \ \ i = -k \\\\k \ \ X \ \ j = -i\\\\i \ \ X \ \ k = - j\\`

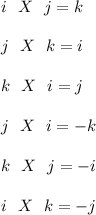
Now force is also mathematically represented as

`F = ma`

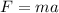
Making a the subject

`a = (F)/(m)`

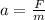
Substituting values

`a =((-5.966*10^4) \r k)/(1.81*10^(-3))`

`= (-0.33m/s^2)\r k`

`= 0.33m/s^2 * (- \r k)`