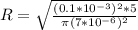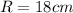Complete Question
A satellite in geostationary orbit is used to transmit data via electromagnetic radiation. The satellite is at a height of 35,000 km above the surface of the earth, and we assume it has an isotropic power output of 1 kW (although, in practice, satellite antennas transmit signals that are less powerful but more directional).
Imagine that the satellite described in the problem introduction is used to transmit television signals. You have a satellite TV reciever consisting of a circular dish of radius R which focuses the electromagnetic energy incident from the satellite onto a receiver which has a surface area of 5 cm2.
How large does the radius R of the dish have to be to achieve an electric field vector amplitude of 0.1 mV/m at the receiver?
For simplicity, assume that your house is located directly beneath the satellite (i.e. the situation you calculated in the first part), that the dish reflects all of the incident signal onto the receiver, and that there are no losses associated with the reception process. The dish has a curvature, but the radius R refers to the projection of the dish into the plane perpendicular to the direction of the incoming signal.
Give your answer in centimeters, to two significant figures.
Answer:
The radius of the dish is
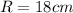
Step-by-step explanation:
From the question we are told that
The radius of the orbit is =
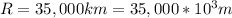
The power output of the power is
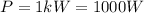
The electric vector amplitude is given as
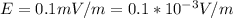
The area of thereciever is
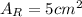
Generally the intensity of the dish is mathematically represented as

Where A is the area orbit which is a sphere so this is obtained as
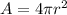
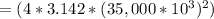
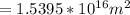
Then substituting into the equation for intensity

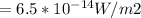
Now the intensity received by the dish can be mathematically evaluated as
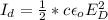
Where c is thesped of light with a constant value

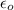 is the permitivity of free space with a value
is the permitivity of free space with a value
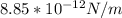
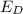 is the electric filed on the dish
is the electric filed on the dish
So since we are to assume to loss then the intensity of the satellite is equal to the intensity incident on the receiver dish
Now making the eletric field intensity the subject of the formula
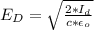
substituting values
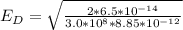

The incident power on the dish is what is been reflected to the receiver
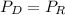
Where
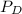 is the power incident on the dish which is mathematically represented as
is the power incident on the dish which is mathematically represented as
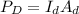
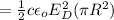
And
 is the power incident on the dish which is mathematically represented as
is the power incident on the dish which is mathematically represented as
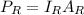
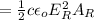
Now equating the two
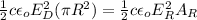
Making R the subject we have
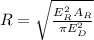
Substituting values