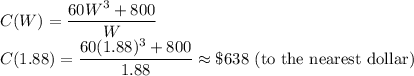Question

In order to package one of their products, Acme Box Co. needs to construct a box whose bottom side has length 3 times its width. The material used to build the top and bottom of the box cost $10 per square foot, while the material used to build the four sides of the box cost $6 per square foot. The box must have a volume of 50 cubic feet. (a) In terms of the length ` of the bottom, the width w of the bottom and the height h of the box (all measured in feet), write a formula for the cost C (in dollars) to construct a box of length `, width w and height h. (b) Given the other conditions specified in the problem, express C as a function of a single variable. (c) Determine the dimensions of the box that minimize the cost. Be sure to justify that you have found dimensions that produce the minimum cost. (You’ll be fired if you submit the maximum cost to your boss!) To the nearest dollar, how much will it cost to build the box at these dimensions?

Answer 1

(a)Total Cost, C=20LW+12LH+12WH

(b)
`C(W)=(60W^3+800)/(W)`

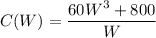
(c)W=1.88ft, L=5.64 ft and H=4.72 ft.

`Minimum \:cost, C\approx \$638 $ (to the nearest dollar)$`

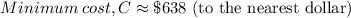
Step-by-step explanation:

Given the dimensions of the box to be L,W and H.

(a)

• The material for the top and bottom of the box cost $10 per square foot
• The material used to build the four sides of the box cost $6 per square foot.
• Area of Top and Bottom=2LW

• Cost of Top and bottom=$10 X 2LW=20LW
• Area of four Sides =2(LH+WH)
• Cost of Four Sides =$6*2(LH+WH)=12(LH+WH)
• Total Cost, C=20LW+12LH+12WH

(b)The bottom side has length 3 times its width.

L=3W

Volume of the box=50 cubic feet.

`Volume,V=LWH=3W^2H`

`3W^2H=50\\H=(50)/(3W^2)`

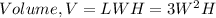
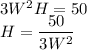
Substituting L=3W and
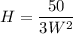`H=(50)/(3W^2)` into the cost function C.

C=20LW+12LH+12WH

`C=20LW+12LH+12WH\\=20*3W*W+12*3W*(50)/(3W^2)+12W*(50)/(3W^2)\\=60W^2+(600)/(W)+(200)/(W)\\=(60W^3+600+200)/(W)\\C(W)=(60W^3+800)/(W)`

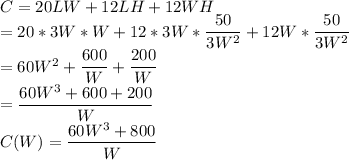
(c)The minimum cost occurs at the point where the derivative of the cost function equals zero.

`If\:C(W)=(60W^3+800)/(W)\\C'(W)=(120W^3-800)/(W^2)=0\\120W^3-800=0\\120W^3=800\\W^3=(800)/(120)\\ W=1.88`

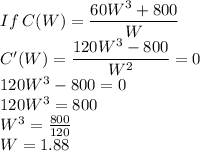
Recall:

`L=3W=5.64 feet\\H=(50)/(3W^2)=(50)/(3(1.88)^2)=4.72 ft`

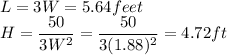
The dimensions of the box that minimize the cost are W=1.88ft, L=5.64 ft and H=4.72 ft.

Cost of the box at these dimension

`C(W)=(60W^3+800)/(W)\\C(1.88)=(60(1.88)^3+800)/(1.88)\approx \$638 $ (to the nearest dollar)$`