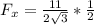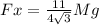Question

A uniform beam with mass M and length L is attached to the wall by a hinge, and supported by a cable. A mass of value 3M is suspended from the bar 3/4ths of its length from the wall. The angle indicated is 60°. What is the tension in the cable? What is the horizontal force provided by the hinge?

Answer 1

The tension is
`T= (11)/(2√(3) ) Mg`

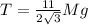
The horizontal force provided by hinge
`Fx= (11)/(4√(3) ) Mg`

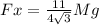
Step-by-step explanation:

From the question we are told that

The mass of the beam is
`m_b =M`

The length of the beam is
`l = L`

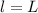
The hanging mass is
`m_h = 3M`

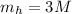
The length of the hannging mass is
`l_h = (3)/(4) l`

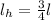
The angle the cable makes with the wall is
`\theta = 60^o`

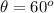
The free body diagram of this setup is shown on the first uploaded image

The force
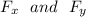`F_x \ \ and \ \ F_y` are the forces experienced by the beam due to the hinges

Looking at the diagram we ca see that the moment of the force about the fixed end of the beam along both the x-axis and the y- axis is zero

So

`\sum F =0`

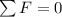
Now about the x-axis the moment is

`F_x -T cos \theta = 0`

=>
`F_x = Tcos \theta`

Substituting values

`F_x =T cos (60)`

`F_x= (T)/(2) ---(1)`

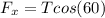
Now about the y-axis the moment is

`F_y + Tsin \theta = M *g + 3M *g ----(2)`

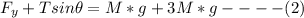
Now the torque on the system is zero because their is no rotation

So the torque above point 0 is

`M* g * (L)/(2) + 3M * g (3L)/(2) - T sin(60) * L = 0`

`(Mg)/(2) + (9 Mg)/(4) - T * (√(3) )/(2) = 0`

`(2Mg + 9Mg)/(4) = T * (√(3) )/(2)`

`T = (11Mg)/(4) * (2)/(√(3) )`

`T= (11)/(2√(3) ) Mg`

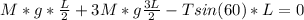
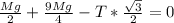
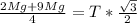
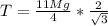
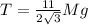
The horizontal force provided by the hinge is

`F_x= (T)/(2) ---(1)`

Now substituting for T

`F_(x) = (11)/(2√(3) ) * (1)/(2)`

`Fx= (11)/(4√(3) ) Mg`