Question

How do i find a,b and k?​

Answer 1

a = 1

b = 2

k = -2

Explanation:

Given:

`\displaystyle \large{y=k(x-a)^2(x-b)}`

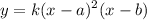
First, find the a-value and b-value by observing the graph. Notice that once the graph hits x = 1, it just goes up or concave up - that indicates to be the double roots of function. Therefore:

Our a-value is 1

Second, find the b-value. Another x-intercept beside double roots x = 1 is x = 2 as shown in the graph. Therefore:

Our b-value is 2

Third, find the k-value. Right now we have the equation:

`\displaystyle \large{y=k(x-1)^2(x-2)}`

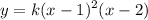
To find the k-value, simply find a point’s value (x,y) to substitute. According to the graph, you can try substitute (0,4) in:

`\displaystyle \large{4=k(0-1)^2(0-2)}\\\displaystyle \large{4=k(-1)^2(-2)}\\\displaystyle \large{4=k(1)(-2)}\\\displaystyle \large{4=-2k}\\\displaystyle \large{k=-2}`

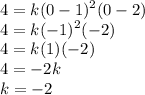
Therefore, the value of k is -2