Question

A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 49.049.0 and 54.054.0 minutes. Find the probability that a given class period runs between 51.2551.25 and 51.7551.75 minutes. Find the probability of selecting a class that runs between 51.2551.25 and 51.7551.75 minutes.

Answer 1

10% probability that a given class period runs between 51.25 and 51.75 minutes.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability of finding a value X between c and d, d greater than c, is given by the following formula:

`P(c \leq X \leq d) = (d-c)/(b-a)`

Uniformly distributed between 49 and 54 minutes

This means that
`b = 54, a = 49`

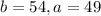
Find the probability that a given class period runs between 51.25 and 51.75 minutes.

`P(51.25 \leq X \leq 51.75) = (51.75 - 51.25)/(54 - 49) = 0.1`

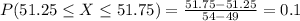
10% probability that a given class period runs between 51.25 and 51.75 minutes.