Question

A sheet of steel 5.0-mm thick has nitrogen atmospheres on both sides at 1000°C and is permitted to achieve a steady-state diffusion condition. The diffusion coefficient for nitrogen in steel at this temperature is 1.95 × 10-10 m2 /s, and the diffusion flux is found to be 1.2 × 10-7 kg/m2.s. Also, it is known that the concentration of nitrogen in the steel at the high-pressure surface is 3 kg/m3 . How far into the sheet from this high-pressure side will the concentration be 0.5 kg/m3 ? Assume a linear concentration profile

Answer 1

The distance from the higher concentration side is
`= 4.06*10^(-3)m`

Step-by-step explanation:

From the question we are told that

The thickness of the steel is
`D = 5.0mm = (5)/(1000) = 5*10^(-3) m`

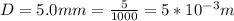
The temperature is
`T = 1000^oC`

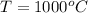
The diffusion coefficient of nitrogen in steel is
`D = 1.95 *10^(-10)m^2/s`

The diffusion flux is
`J = 1.2 *10^(-7)m^2 s`

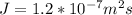
The concentration of nitrogen in steel is
`M = 3kg/m^3`

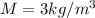
The concentration at distance d is
`M_d = 0.5kg/m^3`

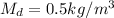
Generally Fick's first law show the relationship between diffusion flux and concentration under an assumption of steady state and this can be represented mathematically as

`J = -D (dC)/(dx)`

Where D is the diffusion coefficient and
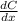`(dC)/(dx)` is the concentration gradient

and J is the diffusion flux

Now if we are considering two concentration the equation for concentration gradient becomes

`(dC)/(dx) = (C_B - C_A )/(x_B - x_A)`

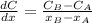
Where
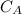`C_A` is the concentraion at high pressure while
`C_B` is concentration at low pressure

`x_A` is the position at the high concentration side

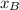`x_B` is the position at the low concentration side

Now sustituting values into the formula for concentration gradient

`(dC)/(dx) = (0.5 - 3)/(x_B -x_A)`

`(dC)/(dx) = (-2.5)/(x_B -x_A)`

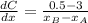
Now substituting values into equation for Fick's law

`1.2*10^(-7) =- 1.95 *10^(-10) (-2.5)/(x_B -x_A)`

`1.2*10^(-7) =(4.875*10^(-10))/(x_B -x_A)`

`x_B - x_A = 4.06 *10^(-3)m`

`x_B = x_A + 4.06 *10^(-3)m`

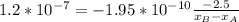
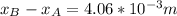
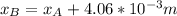
Since the position the higer concentration side from origin is
`x_A` the from the equation we see that the distance of the sheet from the higher concentration side is
`= 4.06*10^(-3)m`