Answer:
38.18% probability that they came from University A
Explanation:
To solve this question, we need to understand the normal probability distribution and the conditional probability formula.
Normal probability distribution:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Conditional probability formula:
We use the conditional probability formula to solve this question. It is
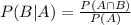
In which
P(B|A) is the probability of event B happening, given that A happened.
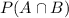 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
If you are told that a graduate is earning less than 35,000, what is the probability that they came from University A
So:
Event A: earning less than 35,000
Event B: coming form university A.
Probability of earning less than 35,000.
40% come from University A.
University A: Mean 30,000 and standard deviation 5,000.
This probability is the pvalue of Z when X = 35,000. So

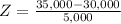
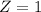
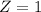 has a pvalue of 0.8413.
has a pvalue of 0.8413.
Intersection is coming from university A and earning less than 35,000. So
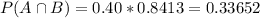
60% come from university B:
Mean 25,000 and standard deviation 7,5000.

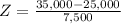

 has a pvalue of 0.9082.
has a pvalue of 0.9082.
Then

Finally:
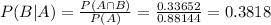
38.18% probability that they came from University A