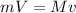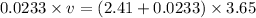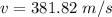Question

A 0.0233-kg bullet is fired horizontally into a 2.41-kg wooden block attached to one end of a massless, horizontal spring (k = 845 N/m). The other end of the spring is fixed in place, and the spring is unstrained initially. The block rests on a horizontal, frictionless surface. The bullet strikes the block perpendicularly and quickly comes to a halt within it. As a result of this completely inelastic collision, the spring is compressed along its axis and causes the block/bullet to oscillate with an amplitude of 0.196 m. What is the speed of the bullet?

Answer 1

`v= 381.82\ m/s`

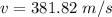
Step-by-step explanation:

Given,

mass of the bullet, m = 0.0233 Kg

Mass of the block, M = 2.41 Kg

horizontal spring constant, k = 845 N/m

Amplitude of oscillation, A = 0.196 m

Using conservation of energy when the bullet is embedded

PE = KE

`(1)/(2)kA^2 = (1)/(2) Mv^2`

`v =A \sqrt{(k)/(M)}`

`v =0.196* \sqrt{(845)/(2.41+0.0233)}`

`v= 3.65\ m/s`

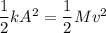
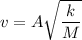
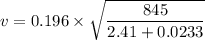
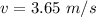
Now using conservation of momentum to calculate the initial velocity of bullet

`m V = M v`

`0.0233* v=(2.41+ 0.0233)* 3.65`

`v= 381.82\ m/s`