Question

2) The results of a 2012 Pew Foundation survey of high school and middle school teachers is given in the pie chart. A student asked a random sample of teachers in 2018 and found 165 had smart-phones, 80 had a cell phone other than smart-phones, and 5 had no cell phone. Is there a difference in the distribution of types of cell phones for the teachers in 2018 at a 5% level of significance?

Answer 1

The calculated value z = 9.4451 > 1.96 at 5% level of significance.

Null hypothesis is rejected at 5% level of significance

yes there is difference in the distribution of types of cell phones for the teachers in 2018 at a 5% level of significance

Explanation:

Explanation:-

Step:- (1)

The results of a 2012 Pew Foundation survey of high school and middle school teachers is given in the pie chart.

A student asked a random sample of teachers in 2018 and found 165 had smart-phones, 80 had a cell phone

The first sample proportion

`p_(1) = (80)/(165) = 0.4848`

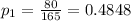
A student asked a random sample of teachers in 2018 and found 165 had smart-phones,5 had no cell phone

The second sample proportion

`p_(2) = (5)/(165) = 0.03030`

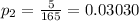
Step :-(ii)

Null hypothesis :H₀: Assume that there is no difference in the distribution of types of cell phones for the teachers in 2018

H₀ : p₁ = p₂

Alternative hypothesis :H₁

H₁ : p₁ ≠ p₂

Level of significance : ∝=0.05

The tabulated value z=1.96

Step:-(iii)

The test statistic

`Z = \frac{p_(1) -p_(2) }{\sqrt{pq((1)/(n_(1) ) } +(1)/(n_(2) ) )} }`

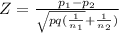
where
`p = (n_(1)p_(1) +n_(2) p_(2) )/(n_(1) + n_(2) )`

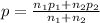
q = 1-p

In given data n₁ = n₂ = n

`p = (165 (0.4848)+165 (0.03030 )/(165 + 165)`

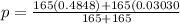
on calculation , we get p = 0.2655

q =1-p = 1-0.2655

q = 0.7345

`Z = \frac{0.4848 -0.030}{\sqrt{0.2655X0.7345((1)/(165 ) } +(1)/(165) )} }`

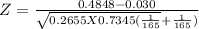
Z = 9.4451

The calculated value z = 9.4451 > 1.96 at 5% level of significance.

Conclusion:-

Null hypothesis is rejected at 5% level of significance

yes there is difference in the distribution of types of cell phones for the teachers in 2018 at a 5% level of significance