Here is the correct question:
The reaction A → products was studied at a series of different temperatures. A plot of ln(k) vs. 1/T gave a straight line relationship with a slope of -693 and a y-intercept of -0.425. Additionally, a study of the concentration of A with respect to time showed that only a plot of 1/[A] vs. time gave a straight line relationship. What is the initial rate of this reaction when [A] = 0.41 at 271 K ?
Answer:
the initial rate of this reaction is 0.0216275 M/sec
Step-by-step explanation:
Using the formula:
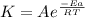
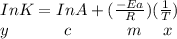
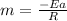
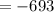
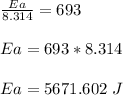
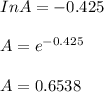
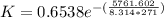
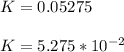
Since
![(1)/([A])](https://img.qammunity.org/2021/formulas/chemistry/college/9xermz2p6fe9n2hjzchp590wq0g9lfp5b3.png) vs time is a straight line relationship;
vs time is a straight line relationship;
Therefore, it is a second order reaction
rate = K[A]²
rate = 5.275 × 10⁻² × (0.41)
rate = 0.0216275 M/sec