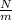Question

A rifle fires a 2.01 10-2-kg pellet straight upward, because the pellet rests on a compressed spring that is released when the trigger is pulled. The spring has a negligible mass and is compressed by 9.45 10-2 m from its unstrained length. The pellet rises to a maximum height of 6.03 m above its position on the compressed spring. Ignoring air resistance, determine the spring constant.

Answer 1

The value of spring constant is 266.01
`(N)/(m)`

Step-by-step explanation:

Given:

Mass of pellet
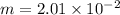`m = 2.01 * 10^(-2)` kg

Height difference of pellet rise
`h_(f) - h_(o) = 6.03` m

Spring compression
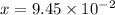`x = 9.45 * 10^(-2)` m

From energy conservation law,

Spring potential energy is stored into potential energy,

`mg(h_(f) -h_(o)) = (1)/(2) kx^(2)`

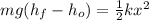
Where
`k =` spring constant,
`g = 9.8 (m)/(s^(2) )`

`k = (2mg(h_(f) -h_(o) ))/(x^(2) )`

`k = (2 * 9.8 * 6.03* 2.01 * 10^(-2) )/((9.45* 10^(-2) )^(2) )`

`k = 266.01`
`(N)/(m)`

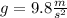
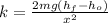
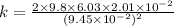
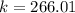
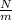
Therefore, the value of spring constant is 266.01
`(N)/(m)`