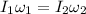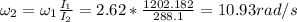Answer:
10.93 rad/s
Step-by-step explanation:
If we treat the student as a point mass, her moment of inertia at the rim is
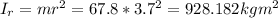
So the system moment of inertia when she's at the rim is:
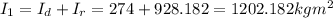
Similarly, we can calculate the system moment of inertia when she's at 0.456 m from the center
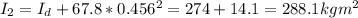
We can apply the law of angular momentum conservation to calculate the post angular speed when she's 0.456m from the center: