Question

A motorboat heads upstream a distance of 24 miles on the Guadeloupe River, whose current is running at 3 mph. The trip up and back takes 6 hours. Assuming that the motorboat maintained a constant speed relative to the water, what was its speed?

Answer 1

9mph

Explanation:

Let speed of boat=x mph

Speed of current=3 mph

Upstream speed=(x-3) mph

Downstream speed =(x+3)mph

Distance=24 miles

Total time=6 hours

`Time=(distance)/(speed)`

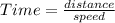
According to question

`(24)/(x+3)+(24)/(x-3)=6`

`(24)(x-3+x+3)/((x+3)(x-3))=6`

`2x(24)=6(x+3)(x-3)`

`(48x)/(6)=x^2-9`

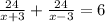
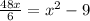
Using the identity:
`(a+b)(a-b)=a^2-b^2`

`8x=x^2-9`

`x^2-8x-9=0`

`x^2-9x+x-9=0`

`x(x-9)+1(x-9)=0`

`(x-9)(x+1)=0`

`x-9=0\implies x=9`

`x+1=0\implies x=-1`

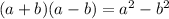
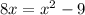
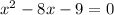
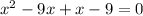
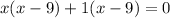
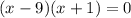
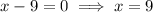
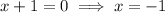
Speed cannot be negative

Therefore, the speed of boat=9mph