Question

Find the value of x.

Answer 1

Given:

Given that the two legs of the triangle are 3 and 4.

The one of the angles of the triangle is x.

We need to determine the measure of x.

Measure of x:

The measure of x can be determined using the trigonometric ratio.

Thus, we have;

`tan \ x=(opp)/(adj)`

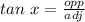
where the side opposite to the angle x is 4 and the side adjacent to the angle x is 3.

Substituting these values, we get;

`tan \ x=(4)/(3)`

`tan \ x=1.33`

`x=tan^(-1)(1.33)`

`x=53.06`

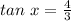
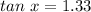
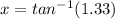
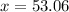
Rounding off to the nearest degree, we get;

`x=53^(\circ)`

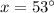
Thus, the measure of x is 53°