Hi there!
Recall that a charge that enters a magnetic field while moving experiences a magnetic force that causes it to enter a state of uniform circular motion.
We know the following (For a point charge):
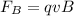
q = Charge (C)
v = velocity (m/s)
B = Magnetic field (T)
Fb= Magnetic force (N)
The equation for centripetal force:
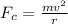
m = mass (kg)
v = velocity (m/s)
r = radius (m)
Fc = Centripetal force (N)
Since we are given its period:
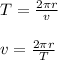
Plug this expression into the above equations. Since the magnetic force equals the centripetal force, set them equal to each other and simplify.
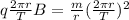
Cancel out the expression.
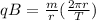
Cancel out 'r'.

Now, we can simplify as necessary to find a value for 'q' over 'm':

Thus, the charge is 1.693 ×10⁶ times larger than its mass.