Question

Based on a​ survey, assume that 2525​% of consumers are comfortable having drones deliver their purchases. Suppose that we want to find the probability that when fivefive consumers are randomly​ selected, exactly threethree of them are comfortable with delivery by drones. Identify the values of​ n, x,​ p, and q.

Answer 1

0.0879 is the probability that out of 5 randomly selected consumers, three are comfortable with delivery by drones.

Explanation:

We are given the following information:

We treat drone deliveries as a success.

P(consumers comfortable having drones deliver) = 25% = 0.25

Then the number of consumers follows a binomial distribution, where

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

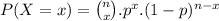
where n is the total number of observations, x is the number of success, p is the probability of success.

We have to evaluate:

P(Exactly 3 customers out of 5 are comfortable with delivery by drones)

Here,

`n = 5\\x = 3\\p = 0.25\\q = 1 - p = 1-0.25=0.75`

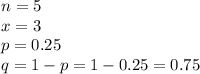
Putting values, we get,

`P(x =3)\\\\= \binom{5}{3}(0.25)^3(1-0.25)^2\\\\= 0.0879`

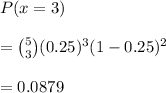
0.0879 is the probability that out of 5 randomly selected consumers, three are comfortable with delivery by drones.