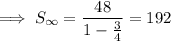Question

Determine whether the infinite geometric series converges or diverges. If it converges, find the sum, and if it diverges then explain why.

48 + 36 + 27 + 81/4 + ...​

Answer 1

Geometric series means

• |r|<1

Lets spot out common ratio

• 36/48=3/4
• 27/36=3/4

Its less than 1

Hence series converges

Sum:-

• a/1-r
• 48/(1-3/4)
• 48/1/4
• 192

Answer 2

Series converges

Sum = 192

Explanation:

General form of geometric series:
`a_n=ar^(n-1)`

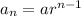
where:

• a is the initial term
• r is the common ratio

Given series: 48, 36, 27, 81/4, ...

`\implies a = 48`

`\implies r=(a_2)/(a_1)=(36)/(48)=\frac34`

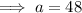
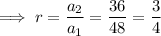
Geometric series converges when |r| < 1

Geometric series diverges when |r| ≥ 1

`\textsf{As }r=\frac34\ \implies|\frac34| < 1\:\implies\:\textsf{series converges}`

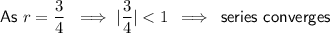
Sum of an infinite geometric series:

`S_\infty=(a)/(1-r)\quad\textsf{for}\:|r| < 1`

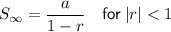
Substituting values of a and r:

`\implies S_\infty=(48)/(1-\frac34)=192`