Answer:
b) 0.9313
c) mean = 2.4
standard deviation= 1.3856
d) 0.5583
Explanation:
Given:
p = 0.2
n = 12
a) X= number of applicants classified as deceptive.
Probability mass function of X will be:
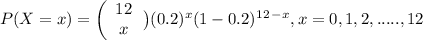
b) Probability that the polygraph says at least 1 is deceptive:
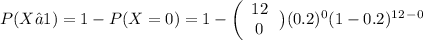
= 1 - 0.0687
= 0.9313
c) The mean number among 12 truthful persons who will be classified as deceptive:
E(X) = n•p
= 12 * 0.2
= 24
Standard deviation:

= 1.3856
d) Probability that the number classified deceptive is less than the mean:
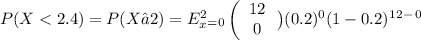
= 0.5583