Question

Interactive Solution 28.5 illustrates one way to model this problem. A 7.11-kg object oscillates back and forth at the end of a spring whose spring constant is 61.6 N/m. An observer is traveling at a speed of 2.79 × 108 m/s relative to the fixed end of the spring. What does this observer measure for the period of oscillation?

Answer 1

Step-by-step explanation:

Given that,

Mass of the object, m = 7.11 kg

Spring constant of the spring, k = 61.6 N/m

Speed of the observer,
`v=2.79* 10^8\ m/s`

We need to find the time period of oscillation observed by the observed. The time period of oscillation is given by :

`t_o=2\pi \sqrt{(m)/(k)} \\\\t_o=2\pi \sqrt{(7.11)/(61.6)} \\\\t_o=2.13\ s`

Time period of oscillation measured by the observer is :

`t=\frac{t_o}{\sqrt{1-(v^2)/(c^2)} }\\\\t=\frac{2.13}{\sqrt{1-((2.79* 10^8)^2)/((3* 10^8)^2)} }\\\\t=5.79\ s`

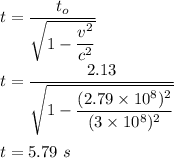
So, the time period of oscillation measured by the observer is 5.79 seconds.