Question

Bond Premium, Entries for Bonds Payable Transactions Campbell Inc. produces and sells outdoor equipment. On July 1, Year 1, Campbell issued $32,000,000 of 10-year, 13% bonds at a market (effective) interest rate of 11%, receiving cash of $35,824,150. Interest on the bonds is payable semiannually on December 31 and June 30. The fiscal year of the company is the calendar year. Required: If an amount box does not require an entry, leave it blank. 1. Journalize the entry to record the amount of cash proceeds from the issuance of the bonds on July 1, Year 1. 2. Journalize the entries to record the following: a. The first semiannual interest payment on December 31, Year 1, and the amortization of the bond premium, using the straight-line method. (Round to the nearest dollar.) b. The interest payment on June 30, Year 2, and the amortization of the bond premium, using the straight-line method. (Round to the nearest dollar.) 3. Determine the total interest expense for Year 1. Round to the nearest dollar. $ 4. Will the bond proceeds always be greater than the face amount of the bonds when the contract rate is greater than the market rate of interest? 5. Compute the price of $35,824,150 received for the bonds by using Exhibit 5 and Exhibit 7. (Round to the nearest dollar.) Your total may vary slightly from the price given due to rounding differences. Present value of the face amount $ Present value of the semi-annual interest payments $ Price received for the bonds $ Check My Work

Answer 1

Using effective -rate:

Cash 35,824,122 debit

Bonds Payable 32,000,000 credit

premium on bonds payable 3,824,122 credit

--to record issuance--

Interest expense 1,970,326.73 debit

premium on BP 109,673.27 debit

cash 2,080,000 credit

--to record first interest payment--

Interest expense 1,976,358.76 debit

premium on BP 103,641.24 debit

interest payable 2,080,000 credit

--to record accrued interest to Dec 31th--

interest expense on first year:

1,970,326.73 + 1,976,358.76 = 3.946.685,49

Using Straight line:

interest expense 1.888.793,9‬ debit

premium on BP 191.206,1‬ debit

cash 2,080,000 credit

--to record first interest payment--

interest expense 1.888.793,9‬ debit

premium on BP 191.206,1‬ debit

interest payable 2,080,000 credit

--to record accrued interest for the second payment--

total interest expense:

1.888.793,9 + 1.888.793,9 = 3.777.587,8‬

4) Yes as investor will be willing to purchase at a higher price until get the market yield

5)

PV coupon payment $ 24,856,795.5687

PV maturity $ 10,967,326.8265

Total $ 35,824,122.3952

Step-by-step explanation:

Present value of the bond is the discounted value of the coupon payment and maturity.

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 2,080,000.000

time 20

rate 0.055

`2080000 * (1-(1+0.055)^(-20) )/(0.055) = PV\\`

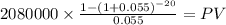
PV $24,856,795.5687

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 32,000,000.00

time 20.00

rate 0.055

`(32000000)/((1 + 0.055)^(20) ) = PV`

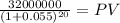
PV 10,967,326.83

PV c $24,856,795.5687

PV m $10,967,326.8265

Total $35,824,122.3952

Then we solve for the effective rate doing carrying value times market:

$35,824,122.3952 x 0.055 = 1,970,326.73

And the cash outlay:

32,000,000 x 0.065 = 2,080,000 debit

The difference is the amortization on premium

The striaght-line will distribute the premium over time equally:

3,824,122 / 20 = 191.206,1

this will be subtracted from the cash outlay to determinatethe interest expense.