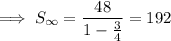Answer:
Series converges
Sum = 192
Explanation:
General form of geometric series:
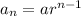
where:
- a is the initial term
- r is the common ratio
Given series: 48, 36, 27, 81/4, ...
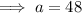
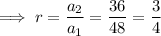
Geometric series converges when |r| < 1
Geometric series diverges when |r| ≥ 1
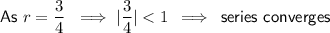
Sum of an infinite geometric series:
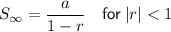
Substituting values of a and r: