Question

Jason's circuit has a 24-Ω resistor that is connected in series to two 12-Ω resistors that are connected in parallel. JoAnna's circuit has three identical resistors wired in parallel. If the equivalent resistance of Jason's circuit is the same as that of JoAnna's circuit, determine the value of JoAnna's resistors.

Answer 1

The value of JoAnna's resistors = 90 Ω

Step-by-step explanation:

Given:

Circuit 1 :

Jason's circuit:

Where Jason/s circuit have three resistor.

One of the resister is, R1 = 24-Ω

Two other two resistor R2 and R3 = 12-Ω and 12-Ω

Lets find the equivalent resistance of Jason's circuit.

⇒ Equivalent resistance,
`R_E` =
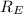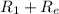`R_1 + R_e` ...equation (i)

⇒
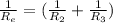`(1)/(R_e) = ((1)/(R_2) + (1)/(R_3))` ...equation (ii)

⇒
`R_e=(R_1* R_2)/(R_1 + R_2)`

⇒
`R_e=(12* 12)/(12 + 12)`

⇒
`R_e=(144)/(24)`

⇒
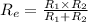
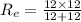
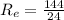
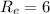`R_e= 6` Ω

Equivalent resistance of Jason's circuit =
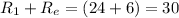`R_1 + R_e =(24+6)=30` Ω

Circuit 2:

JoAnna's circuit :

According to the question :

The equivalent resistance of both the resistor's are same.

Say the resistance are
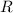`R` and it is equivalent to
`R_E`.

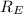And all three resistor are in parallel.

So

⇒
`(1)/(R_E) = (1)/(R) + (1)/(R) + (1)/(R)`

⇒
`(1)/(R_E) = (3)/(R)`

⇒
`R=3* R_E`

⇒
`R=3* 30`

⇒
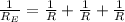
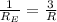
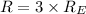
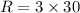
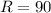`R=90` Ω

The value of JoAnna's resistors = 90 Ω