Question

A local bank has determined that the daily balances of the checking accounts of its customers are normally distributed with an average of $280 and a standard deviation of $20. What percentage of its customers' balances is between $241 and $301.60?

Answer 1

83.43% of customer's balances is between $241 and $301.60.

Explanation:

We are given the following information in the question:

Mean, μ = $280

Standard Deviation, σ = $20

We are given that the distribution of daily balance is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

P(customer's balances is between $241 and $301.60)

`P(241 \leq x \leq 301.60) \\\\= P(\displaystyle(241 - 280)/(20) \leq z \leq \displaystyle(301.60-280)/(20)) \\\\= P(-1.95 \leq z \leq 1.08)\\\\= P(z \leq 1.08) - P(z < -1.95)\\\\= 0.8599 -0.0256 = 0.8343 =83.43\%`

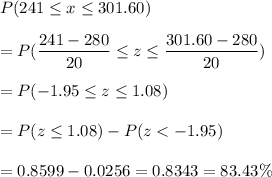
Thus, 83.43% of customer's balances is between $241 and $301.60.