Question

2. The average score of all golfers for a particular course has a mean of 75 and a standard deviation of 4.5. Suppose we going to randomly select 81 golfers and obtain the mean of their scores. We want to know the probability that the average score of the 81 golfers exceeds 76. What would you use on the calculator to find this probability

Answer 1

`P(\bar X>76)`

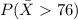
And we can use the z score formula given by:

`z = (\bar X -\mu)/((\sigma)/(√(n)))`

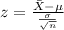
And if we find the z score for 76 we got:

`z =(76-75)/((4.5)/(√(81)))= 2`

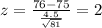
And if we use the complement rule and the normal standard distribution or excel we got:

`P(Z>2) = 1-P(Z<2) = 1- 0.97725= 0.02275`

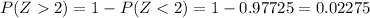
And we can find this using the ti 84 with the following code:

1-normalcdf(-1000, 76, 75, 0.5 )

Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The central limit theorem states that "if we have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large".

Solution to the problem

Let X the random variable who represent the score of golfers. We select a sampel size of 81.

From the central limit theorem we know that the distribution for the sample mean
`\bar X` is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

And we want to find this probability:

`P(\bar X>76)`

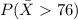
And we can use the z score formula given by:

`z = (\bar X -\mu)/((\sigma)/(√(n)))`

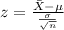
And if we find the z score for 76 we got:

`z =(76-75)/((4.5)/(√(81)))= 2`

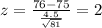
And if we use the complement rule and the normal standard distribution or excel we got:

`P(Z>2) = 1-P(Z<2) = 1- 0.97725= 0.02275`

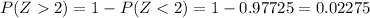
And we can find this using the ti 84 with the following code:

1-normalcdf(-1000, 76, 75, 0.5 )