Question

A heat conducting rod, 0.90 m long, is made of an aluminum section, 0.20 m long, and a copper section, 0.70 m long. Both sections have a cross-sectional area of 0.0004 m^2. The aluminum end and the copper end are maintained at temperatures of 30*C and 230*C respectively. The thermal conductivities of aluminum and copper are 205 and 385 W/m ? K, respectively. The temperature of the aluminum-copper junction in the rod, in *C, is closest to:

Answer 1

is closest to 100*C temperature at the aluminum-copper junction

Step-by-step explanation:

The expression for calculating the resistance of each rod is given by

`R =( L)/( kA)`

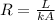
Now; for Aluminium

`R_(al) =( 0.20 )/( 205*0.0004)`

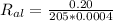
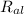`R_(al)` = 2.439

For Copper

`R_(Cu)=(0.70)/(385*0.0004)`

`R_(Cu) = 4.545`

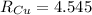
Total Resistance
`R = R_(al) + R_(Cu)`

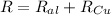
= 2.439 + 4.545

= 6.9845

Total temperature difference = 230*C + 30*C

= 200 *C

The Total rate of heat flow is then determined which is =
`( total \ temp \ difference)/(total \ resistance )`

=
`(200)/( 6.9845 )`

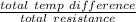
= 28.635 Watts

However. the temperature difference across the aluminium = Heat flow × Resistance of aluminium

= 28.635 × 2.349

= 69.84 *C

Finally. for as much as one end of the aluminium is = 30 *C , the other end is;

=30*C + 69.84*C

= 99.84 *C

which is closest to 100*C temperature at the aluminum-copper junction