Question

(a) Suppose one house from the city will be selected at random. Use the histogram to estimate the probability that the selected house is valued at less than $500,000. Show your work.

(b) Suppose a random sample of 40 houses are selected from the city. Estimate the probability that the mean value of the 40 houses is less than $500,000. Show your work.

Answer 1

a) 0.71

b) 0.9863

Explanation:

a. Given the mean prices of a house is $403,000 and the standard deviation is $278,000

-The probability the probability that the selected house is valued at less than $500,000 is obtained by summing the frequencies of prices below $500,000:

`P(X<500,000)=P(X=0)+P(X=500)\\\\=0.34+0.37\\\\=0.71`

Hence, the probability of a house price below $500,000 is 0.71

b. -Let X be the mean price of a randomly selected house.

-Since the sample size 40 is greater than 30, we assume normal distribution.

-The probability can therefore be calculated as follows:

`P(X<x)=P(z<(\bar X-\mu)/(\sigma/√(n)))\\\\P(X<500,000)=P(z<(500-403)/(278/√(40)))\\\\=P(z<2.2068)\\\\\\=0.9863`

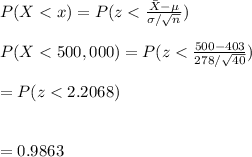
Thus, the probability that the mean value of the 40 houses is less than $500,000 is 0.9863