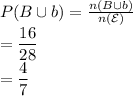Question

In a certain Algebra 2 class of 28 students, 8 of them play basketball and 14 of them play baseball. There are 12 students who play neither sport. What is the probability that a student chosen randomly from the class plays basketball or baseball

Answer 1

4/7

Explanation:

4/7

Answer 2

`P(B \cup b) =(4)/(7)`

Explanation:

Total Number of students, the Universal Set
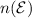`n(\mathcal{E})`=28

Let the number of those who play basketball =B

Let the number of those who play baseball =n

Number who play neither sport,
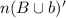`n(B\cup b)'`=12

From Set Theory,

Since we want to determine the probability that a student chosen randomly from the class plays basketball or baseball, we only simply exclude those who play neither sports.

Mathematically,From Set Theory,

`\mathcal{E}=n(B \cup b)+n(B \cup b)'\\28=n(B \cup b)+12\\n(B \cup b)=28-12\\n(B \cup b)=16`

The Probability that a student chosen randomly from the class plays basketball or baseball

`P(B \cup b)=\frac{n(B \cup b)}{n(\mathcal{E})}\\=(16)/(28)\\ =(4)/(7)`