Question

An online retailer wants to estimate the number of visitors that click on their advertisement from a particular website. Of 978 page views in a day, 8% of the users clicked on the advertisement. Create a 90% confidence interval for the population proportion of visitors that click on the advertisement.

Answer 1

(0.0657,0.0943) is the 90% confidence interval for the population proportion of visitors that click on the advertisement.

Explanation:

We are given the following in the question:

Sample size, n = 978

Percentage of users that clicked on advertisement = 8%

Sample proportion:

`\hat{p} = 0.08`

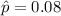
90% Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.10) = 1.645`

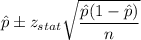
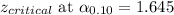
Putting the values, we get:

`0.08\pm 1.645(\sqrt{(0.08(1-0.08))/(978)})\\\\= 0.08\pm 0.0142\\\\=(0.0658,0.0942) = (6.57\%,9.43\%)`

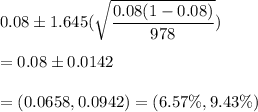
(0.0657,0.0943) is the 90% confidence interval for the population proportion of visitors that click on the advertisement.