Answer:
-(0.330m/s² ) kˆ
Step-by-step explanation:
given data:
Mass of particle 'm'= 1.81 x
 kg
kg
Velocity 'v'= (3.00 x
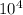 m/s)j
m/s)j
Charge of particle 'q'= 1.22 x
 C
C
Uniform magnetic field 'B' = (1.63iˆ + 0.980jˆ )T
In order to calculate particle's acceleration, we'll use Newton's second law of motion i.e F=ma
Also,the force a magnetic field exerts on a charge q moving with velocity v is called the magnetic Lorentz force. It is given by:
F = qv × B
F= ma = qV x B
a=
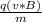 --->eq(1)
--->eq(1)
Lets determine the value of (v x B) first
v x B= (3.00 x
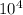 m/s)j x (1.63iˆ + 0.980jˆ )
m/s)j x (1.63iˆ + 0.980jˆ )
v x B= 4.89 x
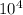
Plugging all the required values in eq(1)
a= [1.22 x
 x (4.89 x
x (4.89 x
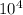 kˆ)] / 1.81 x
kˆ)] / 1.81 x

a= -(0.330m/s² ) kˆ
-ve sign is representing the opposite direction