Question

The tub of a washer goes into its spin-dry cycle, starting from rest and reaching an angular speed of 2.0 rev/s in 10.0 s. At this point, the person doing the laundry opens the lid, and a safety switch turns off the washer. The tub slows to rest in 12.0 s. Through how many revolutions does the tub turn during this 22 s interval? Assume constant angular acceleration while it is starting and stopping.

Answer 1

22 revolutions

Step-by-step explanation:

2 rev/s = 2*(2π rad/rev) = 12.57 rad/s

The angular acceleration when it starting

`\alpha_a = (\Delta \omega)/(\Delta t) = (12.57)/(10) = 1.257 rad/s^2`

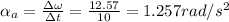
The angular acceleration when it stopping:

`\alpha_o = (\Delta \omega)/(\Delta t) = (-12.57)/(12) = -1.05 rad/s^2`

The angular distance it covers when starting from rest:

`\omega^2 - 0^2 = 2\alpha_a\theta_a`

`\theta_a = (\omega^2)/(2\alpha_a) = (12.57^2)/(2*1.257) = 62.8 rad`

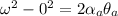
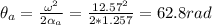
The angular distance it covers when coming to complete stop:

`0 - \omega^2 = 2\alpha_o\theta_o`

`\theta_o = (-\omega^2)/(2\alpha_o) = (-12.57^2)/(2*(-1.05)) = 75.4 rad`

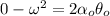
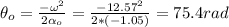
So the total angular distance it covers within 22 s is 62.8 + 75.4 = 138.23 rad or 138.23 / (2π) = 22 revolutions