To solve the problem we will apply the concepts related to the Intensity as a function of the power and the area, as well as the electric field as a function of the current, the speed of light and the permeability in free space, as shown below.
The intensity of the wave at the receiver is
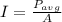
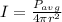
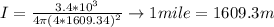
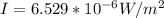
The amplitude of electric field at the receiver is
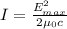
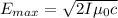
The amplitude of induced emf by this signal between the ends of the receiving antenna is
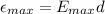
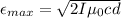
Here,
I = Current
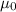 = Permeability at free space
= Permeability at free space
c = Light speed
d = Distance
Replacing,
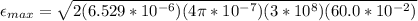
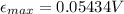
Thus, the amplitude of induced emf by this signal between the ends of the receiving antenna is 0.0543V