Question

The lens-makers’ equation applies to a lens immersed in a liquid if n in the equation is replaced by n2/n1. Here n2 refers to the index of refraction of the lens material and n1 is that of the medium surrounding the lens. (a) A certain lens has focal length 79.0 cm in air and index of refraction 1.55. Find its focal length in water. (b) A certain mirror has focal length 79.0 cm in air. Find its focal length in water.

Answer 1

a

The focal length of the lens in water is
`f_(water) = 262.68 cm`

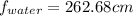
b

The focal length of the mirror in water is
`f =79.0cm`

Step-by-step explanation:

From the question we are told that

The index of refraction of the lens material =
`n_2`

The index of refraction of the medium surrounding the lens =
`n_1`

The lens maker's formula is mathematically represented as

`(1)/(f) = (n -1) [(1)/(R_1) - (1)/(R_2) ]`

Where
`f` is the focal length

`n` is the index of refraction

`R_1 and R_2` are the radius of curvature of sphere 1 and 2 of the lens

From the question When the lens in air we have

`(1)/(f_(air)) = (n-1) [(1)/(R_1) - (1)/(R_2) ]`

When immersed in liquid the formula becomes

`(1)/(f_(water)) = [(n_2)/(n_1) - 1 ] [(1)/(R_1) - (1)/(R_2) ]`

The ratio of the focal length of the the two medium is mathematically evaluated as

`(f_water)/(f_(air)) = (n_2 -1)/([(n_2)/(n_1) - 1] )`

From the question

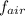`f_(air )`= 79.0 cm

`n_2 = 1.55`

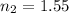
and the refractive index of water(material surrounding the lens) has a constant value of
`n_1 = 1.33`

`(f_(water))/(79) = (1.55- 1)/((1.55)/(1.44) -1)`

`f_(water) = 262.68 cm`

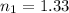
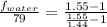
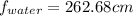
b

The focal length of a mirror is dependent on the concept of reflection which is not affected by medium around it.